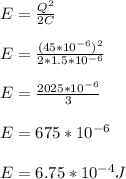Question

An isolated capacitor with capacitance C = 1 µF has a charge Q = 45 µC on its plates.a) What is the energy stored in the capacitor?Now a conductor is inserted into the capacitor. The thickness of the conductor is 1/3 the distance between the plates of the capacitor and is centered inbetween the plates of the capacitor.b) What is the charge on the plates of the capacitor?c) What is the capacitance of the capacitor with the conductor in place?d) What is the energy stored in the capacitor with the conductor in place?

Answer 1

a) Energy stored in the capacitor,
`E = 1.0125 *10^(-3) J`

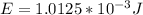
b) Q = 45 µC

c) C' = 1.5 μF

d)
`E = 6.75 *10^(-4) J`

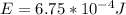
Step-by-step explanation:

Capacitance, C = 1 µF

Charge on the plates, Q = 45 µC

a) Energy stored in the capacitor is given by the formula:

`E = (Q^2)/(2C) \\\\E = ((45 * 10^(-6))^2)/(2* 1* 10^(-6))\\\\E = (2025 * 10^(-6))/(2)\\\\E = 1012.5 *10^(-6)\\\\E = 1.0125 *10^(-3) J`

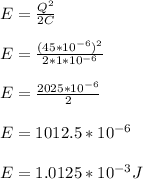
b) The charge on the plates of the capacitor will not change

It will still remains, Q = 45 µC

c) Electric field is non zero over (1-1/3) = 2/3 of d

From the relation V = Ed,

The voltage has changed by a factor of 2/3

Since the capacitance is given as C = Q/V

The new capacitance with the conductor in place, C' = (3/2) C

C' = (3/2) * 1μF

C' = 1.5 μF

d) Energy stored in the capacitor with the conductor in place

`E = (Q^2)/(2C) \\\\E = ((45 * 10^(-6))^2)/(2* 1.5* 10^(-6))\\\\E = (2025 * 10^(-6))/(3)\\\\E = 675 *10^(-6)\\\\E = 6.75 *10^(-4) J`