Question

A seed of CuSO4.5H20 with a mass of 0.500 g was carefully placed into a saturated solution of copper (II) sulfate. After 7 days the mass of the seed crystal was determined to be 0.648 g. After 14 days the mass of the crystal increased to 0.899 g and after 21 days the mass of the crystal was found to be 1.081 g.

Make a plot of mass vs time (days) and extrapolate to predict what would be the mass of the crystal in 28 days if the growth is linear. Include labels and units on each axis.

Answer 1

mass of the gram after 28 days = 1.29 grams

Step-by-step explanation:

From the diagram attached below; we would see the plot of the mass vs the time (days).

However ; to predict what would be the mass of the crystal after 28 days if the growth is linear; we have the following analysis;

Let the mass be Y ( since it falls on the y-axis) and the time (days) be X (since it falls on the x-axis)

So; we can have a table as shown below:

X Y XY XX

0 0.500 0 0

7 0.648 4.536 49

14 0.899 12.586 196

21 1.081 22.701 441

Total
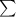`\sum` :42 3.128 39.823 686

If the growth is linear ; the linear regression equation can be represented as :

y = a+ bx

where ;

`a = (\sum Y * \sum XX - \sum X * \sum XY )/(n* \sum X X- ( \sum X)^2)`

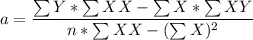
and

`b= (n * \sum XY - \sum X* \sum Y )/(n* \sum X X- ( \sum X)^2)`

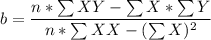
n = samples given = 4

x = number of days = 28

so;

from the table ; replacing the corresponding values; we have:

`a = (3.128* 686 - 42 * 39.823 )/(4* 686- (42)^2)`

`a = (2145.808 -1672.566)/(2744- 1764)`

`a = (473.242)/(980)`

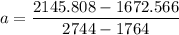
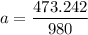
a = 0.4829

`b= (4 * 39.823 - 42* 3.128 )/(4* 686- ( 42)^2)`

`b= (159.292 -131.376 )/(2744- 1764)`

`b= (27.916 )/(980)`

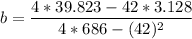
b = 0.0289

Recall:

y = a+ bx

y = 0.4829 + 0.0289 (28)

y = 0.4829 + 0.8092

y = 1.2921 grams

y ≅ 1.29 grams

mass of the gram after 28 days = 1.29 grams