Answer:
mass of the gram after 28 days = 1.29 grams
Step-by-step explanation:
From the diagram attached below; we would see the plot of the mass vs the time (days).
However ; to predict what would be the mass of the crystal after 28 days if the growth is linear; we have the following analysis;
Let the mass be Y ( since it falls on the y-axis) and the time (days) be X (since it falls on the x-axis)
So; we can have a table as shown below:
X Y XY XX
0 0.500 0 0
7 0.648 4.536 49
14 0.899 12.586 196
21 1.081 22.701 441
Total
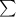 :42 3.128 39.823 686
:42 3.128 39.823 686
If the growth is linear ; the linear regression equation can be represented as :
y = a+ bx
where ;
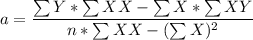
and
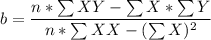
n = samples given = 4
x = number of days = 28
so;
from the table ; replacing the corresponding values; we have:
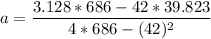
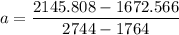
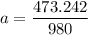
a = 0.4829
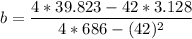
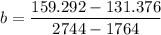
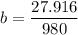
b = 0.0289
Recall:
y = a+ bx
y = 0.4829 + 0.0289 (28)
y = 0.4829 + 0.8092
y = 1.2921 grams
y ≅ 1.29 grams
mass of the gram after 28 days = 1.29 grams