Answer:
Length = 29 m
Width = 29 m
Explanation:
Let x and y be the length and width of the rectangle, respectively.
The area and perimeter are given by:

Rewriting the area as a function of x:

The value of x for which the derivate of the area function is zero, is the length that maximizes the area:
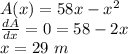
The value of y is:
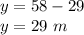
Length = 29 m
Width = 29 m