Find the length and width of a rectangle that has the given perimeter and a maximum area. Perimeter: 116 meters

Question

asked Nov 16, 2021 222k views

1 Answer

Curvin · Answer 1 · 2021-11-21T02:32:15+0000

Answer:

Length = 29 m

Width = 29 m

Explanation:

Let x and y be the length and width of the rectangle, respectively.

The area and perimeter are given by:

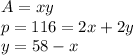
$A=xy\\p=116=2x+2y\\y=58-x$

Rewriting the area as a function of x:

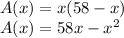
$A(x) = x(58-x)\\A(x) = 58x-x^2$

The value of x for which the derivate of the area function is zero, is the length that maximizes the area:

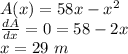
$A(x) = 58x-x^2\\(dA)/(dx)=0=58-2x\\ x=29\ m$

The value of y is:

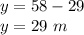
$y = 58-29\\y=29\ m$

Length = 29 m

Width = 29 m