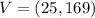Answer:
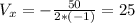
And for the coordinate on y we can use the function like this:
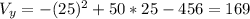
Then the vertex would be
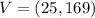
Explanation:
For this problem we have the following function given:
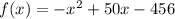
That represent a quadratic function and the general form is given by:
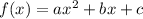
For this problem a =-1 , b= 50 , c=-456 and we can find the corrdinate of the vertex in x with this formula:

And replacing we got:
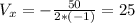
And for the coordinate on y we can use the function like this:
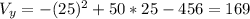
Then the vertex would be