Question

Identify the functions that are continuous on the set of real numbers and arrange them in ascending order of their limits as x tends to 5. Please look at the attached image.

Answer 1

g, j, k, f, m, h

Explanation:

Answer 2

g(x)<j(x)<k(x)<f(x)<m(x)<h(x)

Explanation:

1.
`f(x)=(x^2+x-20)/(x^2+4)`

The denominator of f is defined for all real values of x

Therefore, the function is continuous on the set of real numbers

`\lim_(x\rightarrow 5)(x^2+x-20)/(x^2+4)=(25+5-20)/(25+4)=(10)/(29)=0.345`

3.
`h(x)=(3x-5)/(x^2-5x+7)`

`x^2-5x+7=0`

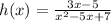
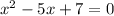
It cannot be factorize .

Therefore, it has no real values for which it is not defined .

Hence, function h is defined for all real values.

`\lim_(x\rightarrow 5)(3x-5)/(x^2-5x+7)=(15-5)/(25-25+7)=(10)/(7)=1.43`

2.
`g(x)=(x-17)/(x^2+75)`

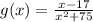
The denominator of g is defined for all real values of x.

Therefore, the function g is continuous on the set of real numbers

`\lim_(x\rightarrow 5)(x-17)/(x^2+75)=(5-17)/(25+75)=(-12)/(100)=-0.12`

4.
`i(x)=(x^2-9)/(x-9)`

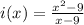
x-9=0

x=9

The function i is not defined for x=9

Therefore, the function i is not continuous on the set of real numbers.

5.
`j(x)=(4x^2-7x-65)/(x^2+10)`

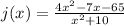
The denominator of j is defined for all real values of x.

Therefore, the function j is continuous on the set of real numbers.

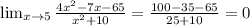
`\lim_(x\rightarrow 5)(4x^2-7x-65)/(x^2+10)=(100-35-65)/(25+10)=0`

6.
`k(x)=(x+1)/(x^2+x+29)`

`x^2+x+29=0`

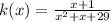
It cannot be factorize .

Therefore, it has no real values for which it is not defined .

Hence, function k is defined for all real values.

`\lim_(x\rightarrow 5)(x+1)/(x^2+x+29)=(5+1)/(25+5+29)=(6)/(59)=0.102`

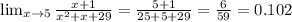
7.
`l(x)=(5x-1)/(x^2-9x+8)`

`x^2-9x+8=0`

`x^2-8x-x+8=0`

`x(x-8)-1(x-8)=0`

`(x-8)(x-1)=0`

`x=8,1`

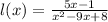
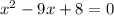
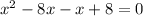
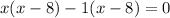
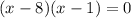
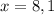
The function is not defined for x=8 and x=1

Hence, function l is not defined for all real values.

8.
`m(x)=(x^2+5x-24)/(x^2+11)`

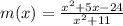
The denominator of m is defined for all real values of x.

Therefore, the function m is continuous on the set of real numbers.

`\lim_(x\rightarrow 5)(x^2+5x-24)/(x^2+11)=(25+25-24)/(25+11)=(26)/(36)=(13)/(18)=0.722`

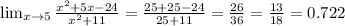
g(x)<j(x)<k(x)<f(x)<m(x)<h(x)