Answer:
(a) The value of a is 53.35.
(b) The value of a is 38.17.
(c) The value of a is 26.95.
(d) The value of a is 25.63.
(e) The value of a is 12.06.
Explanation:
The probability density function of X is:
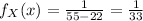
Here, 22 < X < 55.
(a)
Compute the value of a as follows:
![P(X\leq a)=\int\limits^(a)_(22) {(1)/(33)} \, dx \\\\0.95=(1)/(33)\cdot \int\limits^(a)_(22) {1} \, dx \\\\0.95* 33=[x]^(a)_(22)\\\\31.35=a-22\\\\a=31.35+22\\\\a=53.35](https://img.qammunity.org/2021/formulas/mathematics/college/2j3qxrvxqgspihh80wb5a7lfgd4s2kag3t.png)
Thus, the value of a is 53.35.
(b)
Compute the value of a as follows:
![P(X< a)=\int\limits^(a)_(22) {(1)/(33)} \, dx \\\\0.95=(1)/(33)\cdot \int\limits^(a)_(22) {1} \, dx \\\\0.49* 33=[x]^(a)_(22)\\\\16.17=a-22\\\\a=16.17+22\\\\a=38.17](https://img.qammunity.org/2021/formulas/mathematics/college/goj4hf88o97j0lzvl1570pcpqivy3il3wm.png)
Thus, the value of a is 38.17.
(c)
Compute the value of a as follows:
![P(X\geq a)=\int\limits^(55)_(a) {(1)/(33)} \, dx \\\\0.85=(1)/(33)\cdot \int\limits^(55)_(a) {1} \, dx \\\\0.85* 33=[x]^(55)_(a)\\\\28.05=55-a\\\\a=55-28.05\\\\a=26.95](https://img.qammunity.org/2021/formulas/mathematics/college/v0ntcsnzyu1jehw434pdmci03kljyz2baz.png)
Thus, the value of a is 26.95.
(d)
Compute the value of a as follows:
![P(X\geq a)=\int\limits^(55)_(a) {(1)/(33)} \, dx \\\\0.89=(1)/(33)\cdot \int\limits^(55)_(a) {1} \, dx \\\\0.89* 33=[x]^(55)_(a)\\\\29.37=55-a\\\\a=55-29.37\\\\a=25.63](https://img.qammunity.org/2021/formulas/mathematics/college/e4jue0mbs8ptxkbhw5a5yguxm6uh2s6377.png)
Thus, the value of a is 25.63.
(e)
Compute the value of a as follows:
![P(1.83\leq X\leq a)=\int\limits^(a)_(1.83) {(1)/(33)} \, dx \\\\0.31=(1)/(33)\cdot \int\limits^(a)_(1.83) {1} \, dx \\\\0.31* 33=[x]^(a)_(1.83)\\\\10.23=a-1.83\\\\a=10.23+1.83\\\\a=12.06](https://img.qammunity.org/2021/formulas/mathematics/college/vwq2jii8e9xryw9o4np654sh3wt9wfq1a9.png)
Thus, the value of a is 12.06.