Question

Two stationary point charges of 3.00 nC and 2.00 nC are separated by a distance of 60.0 cm. An electron is released from rest at a point midway between the charges and moves along the line connecting them. Part A What is the electric potential energy of the electron when it is at the midpoint

Answer 1

U =-2.39*10^-18 J

Step-by-step explanation:

In order to calculate the electric potential energy of the electron you use the following formula:

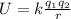`U=k(q_1q_2)/(r)` (1)

k: Coulomb's constant = 8.98*10^9Nm^2/C^2

r: distance between charges

In this case the electron is at point midway between two charges, then the electric potential energy is the sum of two contributions:

`U=U_1+U_2=k(eq_1)/(r)+k(eq_2)/(r)=(ke)/(r)[q_1+q_2]`

e: charge of the electron = 1.6*10^-19C

q1: charge 1 = 3.00nC = 3.00*10^-9C

q2: charge 2 = 2.00nC = 3.00*10^-9C

r: distance to each charge = 60.0cm/2 = 30.0cm = 0.3m

If you consider that the electron is at the origin of coordinates, with the first charge in the negative x axis, and the other one in the positive x axis, you have:

`U=((8.98*10^9Nm^2/C^2)(1.6*10^(-19)C))/(0.6m)[-3.0*10^(-9)C+2.0*10^(-9)C]\\\\U=-2.39*10^(-18)J`

The electric potential energy of the electron is -2.39*10^-18 J