Question

A simple random sample of size nequals17 is drawn from a population that is normally distributed. The sample mean is found to be x overbar equals 56 and the sample standard deviation is found to be sequals10. Construct a 95​% confidence interval about the population mean. The lower bound is nothing. The upper bound is nothing. ​(Round to two decimal places as​ needed.)

Answer 1

95% confidence intervals about the population mean is

(51.7656 , 60.2344)

Explanation:

Step(i):-

Given random sample of size 'n' =17

Given mean of the sample 'x⁻' = 56

Given standard deviation of sample 's' = 10

95% confidence intervals about the population mean is determined by

`(x^(-) - t_(0.05) (s)/(√(n) ) ,x^(-) + t_(0.05) (s)/(√(n) ) )`

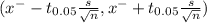
Degrees of freedom

ν = n-1 = 17-1 =16

t₀.₀₅ = 1.7459 (from t-table)

Step(ii):-

95% confidence intervals about the population mean is determined by

`(x^(-) - t_(0.05) (s)/(√(n) ) ,x^(-) + t_(0.05) (s)/(√(n) ) )`

`(56 - 1.7459 (10)/(√(17) ) ,56 + 1.7459 (10)/(√(17) ) )`

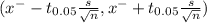
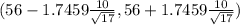
( 56 - 4.2344 , 56 + 4.2344)

(51.7656 , 60.2344)

Conclusion:-

95% confidence intervals about the population mean is

(51.7656 , 60.2344)