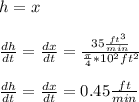Question

Gravel is being dumped from a conveyor belt at a rate of 35 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10 ft high? (Round your answer to two decimal places.)

Answer 1

0.45 ft/min

Explanation:

Given:-

- The flow rate of the gravel,
`(dV)/(dt) = 35 (ft^3)/(min)`

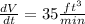
- The base diameter ( d ) of cone = x

- The height ( h ) of cone = x

Find:-

How fast is the height of the pile increasing when the pile is 10 ft high?

Solution:-

- The constant flow rate of gravel dumped onto the conveyor belt is given to be 35 ft^3 / min.

- The gravel pile up into a heap of a conical shape such that base diameter ( d ) and the height ( h ) always remain the same. That is these parameter increase at the same rate.

- We develop a function of volume ( V ) of the heap piled up on conveyor belt in a conical shape as follows:

`V = (\pi )/(12)*d^2*h\\\\V = (\pi )/(12)*x^3`

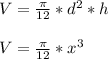
- Now we know that the volume ( V ) is a function of its base diameter and height ( x ). Where x is an implicit function of time ( t ). We will develop a rate of change expression of the volume of gravel piled as follows Use the chain rule of ordinary derivatives:

`(dV)/(dt) = (dV)/(dx) * (dx)/(dt)\\\\(dV)/(dt) = (\pi )/(4) x^2 * (dx)/(dt)\\\\(dx)/(dt) = ((dV)/(dt))/((\pi )/(4) x^2)`

- Determine the rate of change of height ( h ) using the relation developed above when height is 10 ft:

`h = x\\\\(dh)/(dt) = (dx)/(dt) = (35 (ft^3)/(min) )/((\pi )/(4)*10^2 ft^2 ) \\\\(dh)/(dt) = (dx)/(dt) = 0.45 (ft)/(min)`