Question

at needs to determine the height of a tree before cutting it down to be sure that it will not fall on a nearby fence. The angle of elevation of the tree from one position on a flat path from the tree is Upper H equals 60 degrees commaH=60°, and from a second position Upper L equals 20 feetL=20 feet farther along this path it is Upper B equals 40 degrees .B=40°. What is the height of the​ tree?

Answer 1

32.6 feet

Explanation:

The computation of the height of the tree is shown below:

Data provided in the question

One position H = 60 degree

Second position L = 20

B = 40 degree

Based on the above information, the calculations are as follows

In triangle ZWX,

`(h)/(x)=tan(60^(\circ)) => x=(h)/(tan(60^(\circ)))`

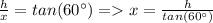
In triangle ZWY

`(h)/(x+L)=tan(40^(\circ)) => h=tan(40^(\circ))(x+20) => x=(h)/(tan(40^(\circ)))-20`

Now from equation 1 and equation 2

`x=(h)/(tan(60^(\circ)))=(h)/(tan(40^(\circ)))-20`

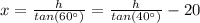
i.e

`20=(h)/(tan(40^(\circ)))-(h)/(tan(60^(\circ))) => h[1.1917535926-0.57735026919]=20`

Hence,

`h=(20)/([1.1917535926-0.57735026919])`

= 32.55190728

= 32.6 feet

Hence, the height of the tree is 32.6 feet