Question

2

The length, width, and height of a
rectangular solid are in the ratio of
3:2:1. If the volume of the box is 48,
what is the total surface area of the box?

Answer 1

88 square units.

Explanation:

Volume of cuboid = length * width *height

total surface area of the = 2*(LB+BH+HL)

where

L = length

B = width

H = Height

_____________________________

Given

The length, width, and height of a

rectangular solid are in the ratio of

3:2:1

let the

length = 3x

width = 2x

and height = x

Volume of box in terms of x = 3x*2x*x =
`6x^3`

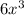
Given that volume if box is 48 cubic units

thus

`6x^3 = 48\\x^3 = 48/6= 8\\x = \sqrt[3]{8} = 2`

Thus,

length = 3x = 3*2 = 6

width = 2x = 2*2 = 4

and height = x = 2

Now

total surface area of the box = 2(6*4 + 4*2+2*6) = 2(24+8+12)

total surface area of the box = 2*44 = 88

Thus, total surface area of the box is 88 square units.