Answer:
The height of the building is approximately 18 meters.
Explanation:
The question is:
FROM THE HIGH PART OF A WALL OF 8M HEIGHT, YOU CAN SEE THE LOW AND HIGH PART OF A BUILDING WITH ELEVATION AND DEPRESSION ANGLES OF 37° AND 45° RESPECTIVELY. CALCULATE THE HEIGHT OF THE BUILDING A.18 B.14 C.12 D.24 E.16
Solution:
Consider the diagram below.
Consider the triangle ABC.
Compute the value of y as follows:
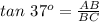
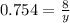
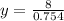
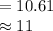
Thus, the length of side AD is also 11 meters.
Now consider the triangle AED.
Compute the value of x as follows:
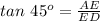
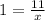
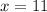
Then the height of the building is:
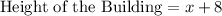
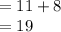
From the options provided it can be concluded that the height of the building is approximately 18 meters.