Question

DESDE LA PARTE ALTA DE UN MURO DE 8M DE ALTURA SE OBSERVA LAS PARTE BAJA Y ALTA DE UN EDIFICIO CON ANGULOS DE ELEVACION Y DEPRESION DE 37 Y 45 RESPECTIVAMENTE. CALCULA LA ALTURA DEL EDIFICIO A.18 B.14 C.12 D.24 E.16

Answer 1

The height of the building is approximately 18 meters.

Explanation:

The question is:

FROM THE HIGH PART OF A WALL OF 8M HEIGHT, YOU CAN SEE THE LOW AND HIGH PART OF A BUILDING WITH ELEVATION AND DEPRESSION ANGLES OF 37° AND 45° RESPECTIVELY. CALCULATE THE HEIGHT OF THE BUILDING A.18 B.14 C.12 D.24 E.16

Solution:

Consider the diagram below.

Consider the triangle ABC.

Compute the value of y as follows:

`tan\ 37^(o)=(AB)/(BC)`

`0.754=(8)/(y)`

`y=(8)/(0.754)`

`=10.61\\\approx 11`

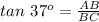
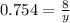
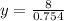
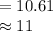
Thus, the length of side AD is also 11 meters.

Now consider the triangle AED.

Compute the value of x as follows:

`tan\ 45^(o)=(AE)/(ED)`

`1=(11)/(x)`

`x=11`

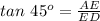
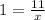
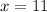
Then the height of the building is:

`\text{Height of the Building}=x+8`

`=11+8\\=19`

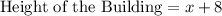
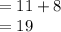
From the options provided it can be concluded that the height of the building is approximately 18 meters.