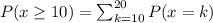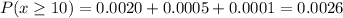Answer:
The probability that you are able to guess ten or more correct answers is P(x≥10) = 0.0026
Explanation:
The question is incomplete:
You take a multiple choice test that you are not prepared for, so you have to guess on all twenty questions. The probability that you guess correctly on any given question is 20% (since there are five choices on each question). What is the probability that you are able to guess ten or more correct answers?
This can be modeled by a binomial random variable, with sample size n=20 and probabillity of success p=0.2.
The probability of guessing k answers right can be calculated as:

We have to calculate the probabiltiy that 10 or more answers are correctly answered guessing: P(x≥10)