Question

A cylindrical tank is required to contain a gage pressure 560 kPa . The tank is to be made of A516 grade 60 steel with a maximum allowable normal stress of 150 MPa . If the inner diameter of the tank is 3 m , what is the minimum thickness, t, of the wall

Answer 1

5.6 mm

Step-by-step explanation:

Given that:

A cylindrical tank is required to contain a:

Gage Pressure P = 560 kPa

Allowable normal stress
`\sigma` = 150 MPa = 150000 Kpa.

The inner diameter of the tank = 3 m

In a closed cylinder there exist both the circumferential stress and the longitudinal stress.

Circumferential stress
`\sigma = (pd)/(2t)`

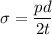
Making thickness t the subject; we have

`t = (pd)/(2* \sigma)`

`t = (560000*3)/(2*150000000)`

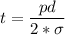
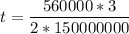
t = 0.0056 m

t = 5.6 mm

For longitudinal stress.

`\sigma = (pd)/(4t)`

`t= (pd)/(4*\sigma )`

`t = (560000*3)/(4*150000000)`

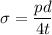
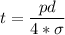
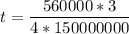
t = 0.0028 mm

t = 2.8 mm

From the above circumferential stress and longitudinal stress; the stress with the higher value will be considered ; which is circumferential stress and it's minimum value with the maximum thickness = 5.6 mm