Question

A pickup truck moves at 25 m/s toward the east. Ahmed is standing in the back and throws a baseball in what to him is the southwest direction at 28 m/s (with respect to the truck). A person at rest on the ground would see the ball moving how fast in what direction? HTML EditorKeyboard Shortcuts

Answer 1

When viewed by a person on the ground, the ball's velocity will be approximately 34.5 m/s towards the southeast.

Step-by-step explanation:

The motion of the ball as viewed by a person on the ground depends on the combined velocities of the pickup truck and the ball. Since the truck is moving at 25 m/s towards the east and the ball is thrown at 28 m/s towards the southwest (with respect to the truck), the ball's velocity will be the vector sum of these velocities. Using vector addition, we find that the ball's velocity with respect to the ground will be approximately 34.5 m/s towards the southeast.

Answer 2

Speed = 20 m/sec at 75 deg South of East = 20 m/sec at 15 deg East of South

Step-by-step explanation:

given data

truck moves = 25 m/s toward the east.

throws a baseball = 28 m/s southwest

solution

first we take here Speed of truck w.r.to ground i.e. V(p/g) = 25 m/sec toward the east so we can say

V(p/g) = (25 i) m/sec ........................1

and

Speed of baseball w.r.t. pickup i.e. V(b/p) = 28 m/sec toward the South West and we know that south west direction is in third quadrant

and here both component (x and y) are negative

So that we can say it

V(b/p) = -28 × cos(45) i - 28 × sin(45) j = -19.8 i - 19.8 j

and

now we use here relative motion velocity for ball w.r.t ground

V(b/g) = V(b/p) + V(p/g ) ..........................2

put here value and we get

V(b/g) = (-19.8 i - 19.8 j) + 25 i = 5.2 i - 19.8 j

so

Magnitude of that velocity

| V(b/g) | =
`√((5.2^2 + 19.8^2))`

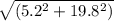
| V(b/g) | = 20.47 m/sec

so that Direction will be here

Direction = arctan (19.8 ÷ 5.2)

Direction = 75.3° South of East

so that

Speed = 20.47 m/sec at 75.3 deg South of East

and 2 significant

Speed = 20 m/sec at 75 deg South of East = 20 m/sec at 15 deg East of South