Question

A linear function has an x-intercept of 12 and a slope of StartFraction 3 Over 8 EndFraction. How does this function compare to the linear function that is represented by the table? x y Negative two-thirds Negative three-fourths Negative one-sixth Negative StartFraction 9 Over 16 EndFraction One-third Negative StartFraction 3 Over 8 EndFraction StartFraction 5 Over 6 EndFraction Negative StartFraction 3 Over 16 EndFraction It has the same slope and the same y-intercept. It has the same slope and a different y-intercept. It has the same y-intercept and a different slope. It has a different slope and a different y-intercept.

Answer 1

B

It has the same slope and a different y-intercept

Explanation:

please rate and ❤️❤️❤️

Answer 2

(B) It has the same slope and a different y-intercept

Explanation:

The table is presented below:

`\left|\begin{array}cx&y\\----&---\\-(2)/(3) &-(3)/(4)\\\\-(1)/(6)&-(9)/(16)\\\\(1)/(3)&-(3)/(8)\\\\(5)/(6)&-(3)/(16)\end{array}\right|`

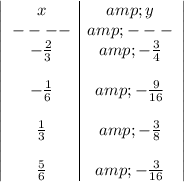
Gradient

`m=(-(3)/(8)-(-(3)/(4)))/((1)/(3)-(-(2)/(3)))\\=(-(3)/(8)+(3)/(4))/((1)/(3)+(2)/(3))\\=(3)/(8)/ (3)/(3)\\m=(3)/(8)`

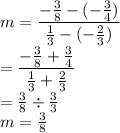
Next, we determine its y-intercept

Using the pair
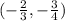`(-(2)/(3),-(3)/(4))` in y=mx+b

`-(3)/(4)=((3)/(8))(-(2)/(3))+b\\-(3)/(4)+(1)/(4)=b\\b=-(1)/(2)`

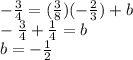
Comparing with the linear function has an x-intercept of 12 and a slope of
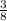`(3)/(8)`, we find out that It has the same slope and a different y-intercept.

Option B is the correct option.