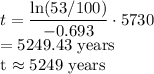Answer:
5249 years
Explanation:
Half-Life of Carbon-14 is approximately 5730 years.
When we want to determine the age of a fossil using carbon dating, we use the formula:
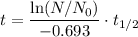
Where:
 is the half-life of the isotope carbon 14,
is the half-life of the isotope carbon 14, - t = age of the fossil (or the date of death) and
- ln() is the natural logarithm function
In this case:
N(t)=100
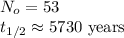
Therefore, the age of the mummy