Question

foot locker uses sales per square foot as a measure of store productivity last year the mean annual sales per square foot was 390 with a standar deviation of 45.83. suppose you take a random sample of 49 foot locker stores operating last year. there is a 82% probability that th esample mean annual sales per square foot is at least $

Answer 1

There is a 82% probability that th esample mean annual sales per square foot is at least $384.

Explanation:

We have a population with mean 390 and standard deviation 45.83.

Samples of size n=49 are taken.

The parameters of the sampling distribution are:

`\mu_s=\mu=390\\\\ \sigma_s=(\sigma)/(√(n))=(45.83)/(√(49))=(45.83)/(7)=6.547`

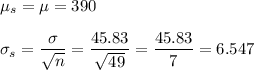
First, we have to calculate the z-score that satisfies:

`P(z>z^*)=0.82`

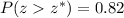
This z-score, looked up in a standard normal distribution table, is z=-0.915.

Then, we can calculate the sample mean as:

`M=\mu_s+z\cdot\sigma_s=390+(-0.915)\cdot 6.547=390-6=384`

There is a 82% probability that th esample mean annual sales per square foot is at least $384.