Question

Students all over the United States recently took the National Science Foundation test on Biology. The mean score for girls was 150, with a standard deviation of 30. What is the approximate percentile rank for a student with a score of 180

Answer 1

`z=(180-150)/(30)= 1`

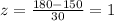
And if we find the probability using the normal standard distribution we got:

`P(z<1)=0.841`

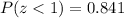
And the the percentile would be approximately 84.1

Explanation:

For this case we define the random variable of interest as "Score for girls" and we know the following parameters:

`\mu =150, \sigma =30`

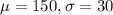
And we want to find the percentile for the score 180 and we can use the z score formula given by:

`z=(X -\mu)/(\sigma)`

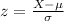
And replacing we got:

`z=(180-150)/(30)= 1`

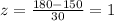
And if we find the probability using the normal standard distribution we got:

`P(z<1)=0.841`

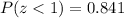
And the the percentile would be approximately 84.1