Find m∠BOC, if m∠MOP = 110°.
Answer:
m∠BOC= 40 degrees
Explanation:
A diagram has been drawn and attached below.
- OM bisects AOB into angles x and x respectively
- ON bisects ∠BOC into angles y and y respectively
- OP bisects ∠COD into angles z and z respectively.
Since ∠AOD is a straight line
x+x+y+y+z+z=180 degrees
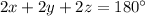
We are given that:
m∠MOP = 110°.
From the diagram
∠MOP=x+2y+z
Therefore:
x+2y+z=110°.
Solving simultaneously by subtraction
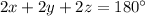
x+2y+z=110°.
We obtain:
x+z=70°
Since we are required to find ∠BOC
∠BOC=2y
Therefore from x+2y+z=110° (since x+z=70°)
70+2y=110
2y=110-70
2y=40
Therefore:
m∠BOC= 40 degrees