Question

OM , ON and OP are the angle bisectors of ∠AOB, ∠BOC, and ∠COD respectively. ∠AOD and ∠BOE are straight angles.

Answer 1

Find m∠BOC, if m∠MOP = 110°.

Answer:

m∠BOC= 40 degrees

Explanation:

A diagram has been drawn and attached below.

• OM bisects AOB into angles x and x respectively
• ON bisects ∠BOC into angles y and y respectively
• OP bisects ∠COD into angles z and z respectively.

Since ∠AOD is a straight line

x+x+y+y+z+z=180 degrees

`2x+2y+2z=180^\circ`

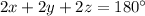
We are given that:

m∠MOP = 110°.

From the diagram

∠MOP=x+2y+z

Therefore:

x+2y+z=110°.

Solving simultaneously by subtraction

`2x+2y+2z=180^\circ`

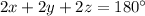
x+2y+z=110°.

We obtain:

x+z=70°

Since we are required to find ∠BOC

∠BOC=2y

Therefore from x+2y+z=110° (since x+z=70°)

70+2y=110

2y=110-70

2y=40

Therefore:

m∠BOC= 40 degrees