Answer:
10 + 7 + 4 + . . .; n = 5
The series is arithmetic
Common difference between terms = (-3)
10 - 3 = 7
7 - 3 = 4
Or:
10 + (-3) = 7
7 + (-3) = 4
--------------------------------------------------------------------------
Another example:
Arithmetic:
5, 9, 13, 17
common difference = 4
5 + 4 = 9
9 + 4 = 13
Geometric:
4, 8, 16, 32
4 × 2 = 8
8 × 2 = 16
16 × 2 = 32
common ratio = 2
--------------------------------------------------------------------------
10 + 7 + 4 + . . .; n = 5
a₁ = 10
a₂ = 7
a₄ = a₃ + d = 4 + (-3) = 4 - 3 = 1 (d = common difference)
a₅ = a₄ - 3 = 1 - 3 = -2
Or with formula:
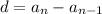
d = a₂ - a₁ = 7 - 10 = -3
aₙ = a₁ + (n - 1)d
fourth term = a₄ = 10 + (4 - 1)(-3) = 10 + 3(-3) = 10 + (-9) = 10 - 9 = 1
fifth term = a₅ = 10 + (5 - 1)(-3) = 10 + 4(-3) = 10 + (-12) = 10 - 12 = -2
Sum of the finite series (if n = 5):
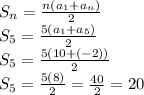
Manual count: S₅ = 10 + 7 + 4 + 1 + (-2) = 20