Question

Determine whether the series is arithmetic or geometric. Then evaluate the finite series for the specified number of terms. 10 + 7 + 4 + . . .; n = 5​

Answer 1

10 + 7 + 4 + . . .; n = 5​

The series is arithmetic

Common difference between terms = (-3)

10 - 3 = 7

7 - 3 = 4

Or:

10 + (-3) = 7

7 + (-3) = 4

--------------------------------------------------------------------------

Another example:

Arithmetic:

5, 9, 13, 17

common difference = 4

5 + 4 = 9

9 + 4 = 13

Geometric:

4, 8, 16, 32

4 × 2 = 8

8 × 2 = 16

16 × 2 = 32

common ratio = 2

--------------------------------------------------------------------------

10 + 7 + 4 + . . .; n = 5​

a₁ = 10

a₂ = 7

a₄ = a₃ + d = 4 + (-3) = 4 - 3 = 1 (d = common difference)

a₅ = a₄ - 3 = 1 - 3 = -2

Or with formula:

`d=a_(n) -a_(n-1)`

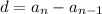
d = a₂ - a₁ = 7 - 10 = -3

aₙ = a₁ + (n - 1)d

fourth term = a₄ = 10 + (4 - 1)(-3) = 10 + 3(-3) = 10 + (-9) = 10 - 9 = 1

fifth term = a₅ = 10 + (5 - 1)(-3) = 10 + 4(-3) = 10 + (-12) = 10 - 12 = -2

Sum of the finite series (if n = 5):

`S_(n) =(n(a_(1) +a_(n) ))/(2) \\S_(5) =(5(a_(1) +a_(5) ))/(2) \\S_(5) =(5(10 +(-2) ))/(2) \\S_(5) =(5(8 ))/(2) =(40)/(2) =20`

Manual count: S₅ = 10 + 7 + 4 + 1 + (-2) = 20