Question

Use the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about the specified axis. y = 11x − x^2, y = 28; about x = 4

Answer 1

27π/2

Explanation:

The differential of volume is the product of a differential of area and the circumference of the revolution of that area about the given axis. The limits of integration in the x-direction are where y=28 crosses the curve, at x=4 and x=7.

`dV=2\pi(x-4)(y-28)\,dx\\\\dV=2\pi(x-4)(-x^2+11x-28)\,dx=2\pi(-x^3+15x^2-72x+112)\,dx\\\\\displaystyle V=\int_4^7{dV}=2\pi\int_4^7{(-x^3+15x^2-72x+112)}\,dx\\\\=2\pi\left((4^4-7^4)/(4)+15(7^3-4^3)/(3)-72(7^2-4^2)/(2)+112(7-4)\right)=2\pi(27)/(4)\\\\\boxed{V=(27\pi)/(2)}`

_____

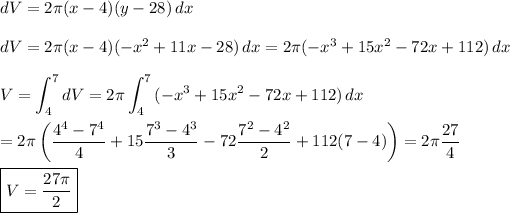
Check

The parabola's vertex is (5.5, 30.25), so its area above the line y=28 is ...

A = (2/3)(7 -4)(30.25 -28) = 4.5 . . . square units

The centroid of that area lies on the line x=5.5, a distance of 1.5 from the axis of rotation. So, the volume of revolution is ...

V = 2π(1.5)(4.5) = 27π/2 . . . matches the above