Answer:
Option (1)
Explanation:
Given triangle ABC shows the length of side AB = 3 units
Measure of angle A = 66°
Measure of angle C = 38°
By applying Sine rule in the given triangle,
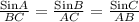
Or

By substituting the given measures,
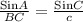
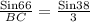
BC =
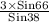
Therefore, Option (1) will be the answer.