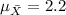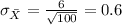Question

The number of violent crimes committed in a day possesses a distribution with a mean of 2.2 crimes per day and a standard deviation of 6 crimes per day. A random sample of 100 days was observed, and the mean number of crimes for the sample was calculated. Describe the sampling distribution of the sample mean. Group of answer choices

Answer 1

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

And replacing we got:

`\mu_(\bar X)= 2.2`

`\sigma_(\bar X)= (6)/(√(100))= 0.6`

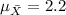
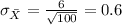
Explanation:

For this case we have the following info given:

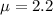`\mu = 2.2` represent the mean

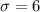`\sigma = 6` represent the deviation

We select a sample size of n=100. This sample is >30 so then we can use the central limit theorem. And we want to find the distribution for the sample mean and we know that the distribution is given by:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

And replacing we got:

`\mu_(\bar X)= 2.2`

`\sigma_(\bar X)= (6)/(√(100))= 0.6`