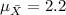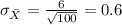Answer:
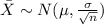
And replacing we got:
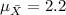
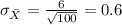
Explanation:
For this case we have the following info given:
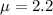 represent the mean
represent the mean
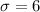 represent the deviation
represent the deviation
We select a sample size of n=100. This sample is >30 so then we can use the central limit theorem. And we want to find the distribution for the sample mean and we know that the distribution is given by:
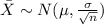
And replacing we got: