Simple and easy question please help

Question

asked Jul 22, 2021 113k views

2 Answers

Minjeong · Answer 1 · 2021-07-26T08:14:16+0000

Answer:

Total volume of the figure = 1067 cm³

Explanation:

Volume of the composite figure = Volume of the rectangular prism + Volume of the square pyramid

Volume of the rectangular prism = Length × Width × Height

= 10 × 10 × 7

= 700 cm³

Volume of the square pyramid =
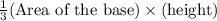
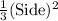$(1)/(3)(\text{Area of the base})* (\text{height})$

=
$(1)/(3)(\text{Side})^2$ × height

=
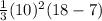
(1)/(3)(10)^2(18-7)

= 366.67 cm³

Total volume of the composite figure = 700 + 366.67 = 1066.67 cm³

≈ 1067 cm³