Question

42:28

Points E, F and D are on circle C, and angle G
measures 60° The measure of arc Ef equals the
measure of arc FD
Which statements about the arcs and angles are
true? Select three options
EFD » LEGD
E
EGD ECD
EDAD
F
DSC0
G609
MET = 60°
MED = 120
Mark this and retum
Save and Exit
Next
Submit

Answer 1

1,3,5

Explanation:

right on edge 2022

Answer 2

The statements about arcs and angles that are true in the figure are;

1) ∠EFD ≅ ∠EGD

2)
`\overline{ED}\cong \overline{FD}`

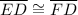
3) mFD = 120°

Explanation:

1) ∠ECD + ∠CEG + ∠CDG + ∠GDE = 360° (Sum of interior angle of a quadrilateral)

∠CEG = ∠CDG = 90° (Given)

∠GDE = 60° (Given)

∴ ∠ECD = 360° - (∠CEG + ∠CDG + ∠GDE)

∠ECD = 360° - (90° + 90° + 60°) = 120°

∠ECD = 2 × ∠EFD (Angle subtended is twice the angle subtended at the circumference)

120° = 2 × ∠EFD

∠EFD = 120°/2 = 60°

∠EFD ≅ ∠EGD

∠ECD = 120°

∠EGD = 60°

∴∠EGD ≠ ∠ECD

2) Given that arc mEF ≅ arc mFD

Therefore, ΔECF and ΔDCF are isosceles triangles having two sides (radii EC and CF in ΔECF and radii EF and CD in ΔDCF

∠ECF = mEF = mFD = ∠DCF (Given)

∴ ΔECF ≅ ΔDCF (Side Angle Side, SAS, rule of congruency)

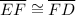`\\ \overline{EF}\cong \overline{FD}` (Corresponding Parts of Congruent Triangles are Congruent, CPCTC)

∠FED ≅ ∠FDE (base angles of isosceles triangle)

∠FED + ∠FDE + ∠EFD = 180° (sum of interior angles of a triangle)

∠FED + ∠FDE = 180° - ∠EFD = 180° - 60° = 120°

∠FED + ∠FDE = 120° = ∠FED + ∠FED (substitution)

2 × ∠FED = 120°

∠FED = 120°/2 = 60° = ∠FDE

∴ ∠FED = ∠FDE = ∠EFD = 60°

ΔEFD is an equilateral triangle as all interior angles are equal

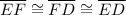`\\ \overline{EF}\cong \overline{FD}\cong \overline{ED}` (definition of equilateral triangle)

`\overline{ED}\cong \overline{FD}`

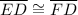
3) Having that ∠EFD = 60° and ∠CFE = ∠CFD (CPCTC)

Where, ∠EFD = ∠CFE + ∠CFD (Angle addition)

60° = ∠CFE + ∠CFD = ∠CFE + ∠CFE (substitution)

60° = 2 × ∠CFE

∠CFE =60°/2 = 30° = ∠CFD

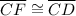`\overline{CF}\cong \overline{CD}` (radii of the same circle)

ΔFCD is an isosceles triangle (definition)

∠CFD ≅ ∠CDF (base angles of isosceles ΔFCD)

∠CFD + ∠CDF + ∠DCF = 180°

∠DCF = 180° - (∠CFD + ∠CDF) = 180° - (30° + 30°) = 120°

mFD = ∠DCF (definition)

mFD = 120°.