Answer:
The statements about arcs and angles that are true in the figure are;
1) ∠EFD ≅ ∠EGD
2)
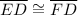
3) mFD = 120°
Explanation:
1) ∠ECD + ∠CEG + ∠CDG + ∠GDE = 360° (Sum of interior angle of a quadrilateral)
∠CEG = ∠CDG = 90° (Given)
∠GDE = 60° (Given)
∴ ∠ECD = 360° - (∠CEG + ∠CDG + ∠GDE)
∠ECD = 360° - (90° + 90° + 60°) = 120°
∠ECD = 2 × ∠EFD (Angle subtended is twice the angle subtended at the circumference)
120° = 2 × ∠EFD
∠EFD = 120°/2 = 60°
∠EFD ≅ ∠EGD
∠ECD = 120°
∠EGD = 60°
∴∠EGD ≠ ∠ECD
2) Given that arc mEF ≅ arc mFD
Therefore, ΔECF and ΔDCF are isosceles triangles having two sides (radii EC and CF in ΔECF and radii EF and CD in ΔDCF
∠ECF = mEF = mFD = ∠DCF (Given)
∴ ΔECF ≅ ΔDCF (Side Angle Side, SAS, rule of congruency)
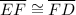 (Corresponding Parts of Congruent Triangles are Congruent, CPCTC)
(Corresponding Parts of Congruent Triangles are Congruent, CPCTC)
∠FED ≅ ∠FDE (base angles of isosceles triangle)
∠FED + ∠FDE + ∠EFD = 180° (sum of interior angles of a triangle)
∠FED + ∠FDE = 180° - ∠EFD = 180° - 60° = 120°
∠FED + ∠FDE = 120° = ∠FED + ∠FED (substitution)
2 × ∠FED = 120°
∠FED = 120°/2 = 60° = ∠FDE
∴ ∠FED = ∠FDE = ∠EFD = 60°
ΔEFD is an equilateral triangle as all interior angles are equal
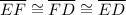 (definition of equilateral triangle)
(definition of equilateral triangle)
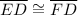
3) Having that ∠EFD = 60° and ∠CFE = ∠CFD (CPCTC)
Where, ∠EFD = ∠CFE + ∠CFD (Angle addition)
60° = ∠CFE + ∠CFD = ∠CFE + ∠CFE (substitution)
60° = 2 × ∠CFE
∠CFE =60°/2 = 30° = ∠CFD
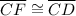 (radii of the same circle)
(radii of the same circle)
ΔFCD is an isosceles triangle (definition)
∠CFD ≅ ∠CDF (base angles of isosceles ΔFCD)
∠CFD + ∠CDF + ∠DCF = 180°
∠DCF = 180° - (∠CFD + ∠CDF) = 180° - (30° + 30°) = 120°
mFD = ∠DCF (definition)
mFD = 120°.