Answer:
Therefore, the sampling distribution of
 is normal with a mean equal to 9 hours and a standard deviation of 0.7969 hours.
is normal with a mean equal to 9 hours and a standard deviation of 0.7969 hours.
The 95% interval estimate of the population mean
 is
is
LCL = 7.431 hours to UCL = 10.569 hours
Explanation:
Let X be the number of hours a legal professional works on a typical workday. Imagine that X is normally distributed with a known standard deviation of 12.6.
The population standard deviation is
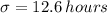
A sample of 250 legal professionals was surveyed, and the sample's mean response was 9 hours.
The sample size is
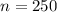
The sample mean is
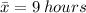
Since the sample size is quite large then according to the central limit theorem, the sample mean is approximately normally distributed.
The population mean would be the same as the sample mean that is
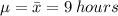
The sample standard deviation would be
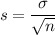
Where is the population standard deviation and n is the sample size.

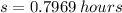
Therefore, the sampling distribution of
 is normal with a mean equal to 9 hours and a standard deviation of 0.7969 hours.
is normal with a mean equal to 9 hours and a standard deviation of 0.7969 hours.
The population mean confidence interval is given by
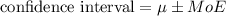
Where the margin of error is given by
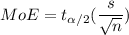
Where n is the sampling size, s is the sample standard deviation and is the t-score corresponding to a 95% confidence level.
The t-score corresponding to a 95% confidence level is
Significance level = α = 1 - 0.95 = 0.05/2 = 0.025
Degree of freedom = n - 1 = 250 - 1 = 249
From the t-table at α = 0.025 and DoF = 249
t-score = 1.9695
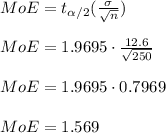
So the required 95% confidence interval is

The 95% interval estimate of the population mean
 is
is
LCL = 7.431 hours to UCL = 10.569 hours