Answer:
C) (-2, 4), (6,8) is the correct answer.
Explanation:
Given that line segment AB:
A (-3, 6) and B (9, 12) is dilated with a scale factor 2/3 about the origin.
First of all, let us calculate the distance AB using the distance formula:
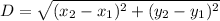
Here,
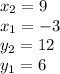
Putting all the values and finding AB:
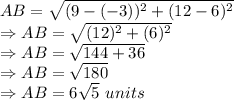
It is given that AB is dilated with a scale factor of
 .
.
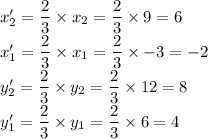
So, the new coordinates are A'(-2,4) and B'(6,8).
Verifying this by calculating the distance A'B':
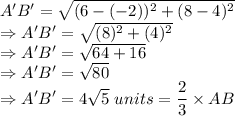
So, option C) (-2, 4), (6,8) is the correct answer.