Question

The line segment AB with endpoints A (-3, 6) and B (9, 12) is dilated with a scale

factor 2/3 about the origin. Find the endpoints of the dilated line segment.

O A) (2, 4), (6,8)

B) (4, -2), (6,8)

O C) (-2, 4), (6,8)

OD) (-2, 4), (8,6)

Answer 1

C) (-2, 4), (6,8) is the correct answer.

Explanation:

Given that line segment AB:

A (-3, 6) and B (9, 12) is dilated with a scale factor 2/3 about the origin.

First of all, let us calculate the distance AB using the distance formula:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

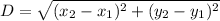
Here,

`x_2=9\\x_1=-3\\y_2=12\\y_1=6`

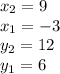
Putting all the values and finding AB:

`AB = √((9-(-3))^2+(12-6)^2)\\\Rightarrow AB = √((12)^2+(6)^2)\\\Rightarrow AB = √(144+36)\\\Rightarrow AB = √(180)\\\Rightarrow AB = 6√(5)\ units`

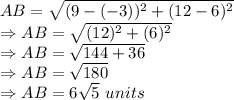
It is given that AB is dilated with a scale factor of
`(2)/(3)`.

`x_2'=(2)/(3)* x_2=(2)/(3)*9=6\\x_1'=(2)/(3)* x_1=(2)/(3)*-3=-2\\y_2'=(2)/(3)* y_2=(2)/(3)* 12=8\\y_1'=(2)/(3)* y_1=(2)/(3)* 6=4`

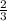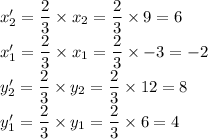
So, the new coordinates are A'(-2,4) and B'(6,8).

Verifying this by calculating the distance A'B':

`A'B' = √((6-(-2))^2+(8-4)^2)\\\Rightarrow A'B' = √((8)^2+(4)^2)\\\Rightarrow A'B' = √(64+16)\\\Rightarrow A'B' = √(80)\\\Rightarrow A'B' = 4√(5)\ units = (2)/(3)* AB`

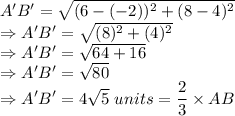
So, option C) (-2, 4), (6,8) is the correct answer.