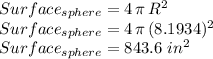Answer:
The surface area of the sphere is:
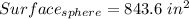
Explanation:
Recall the two following important formulas:
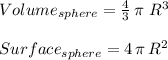
where R is the radius of the sphere.
Then, since we know the sphere's volume (2304
 ), we can calculate the sphere's radius:
), we can calculate the sphere's radius:
![Volume_(sphere)=(4)/(3) \,\pi\,\,R^3\\2304=(4)/(3) \,\pi\,\,R^3\\(3\,*\,2304)/(4\,\pi) =R^3\\R=\sqrt[3]{(6912)/(4\,\pi) } \, in\\R=8.1934\,\, in](https://img.qammunity.org/2021/formulas/mathematics/high-school/z57uf8lkr2m6z4aop1b2habd8yheik1gc8.png)
Now, knowing the radius, we can estimate the surface of the sphere using the other formula;