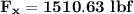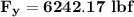Answer:
the restraining forces in the x and y-directions are :
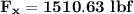
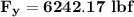
Step-by-step explanation:
From the given information;
Let us first calculate the outlet velocity by using continuity equation.
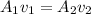
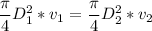
where;
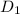 = inlet diameter = 6 - In
= inlet diameter = 6 - In
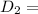 outlet diameter = 4 -In
outlet diameter = 4 -In
inlet velocity
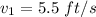
outlet velocity = ???
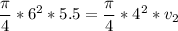
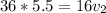
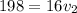
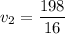
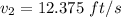 to In; we have
to In; we have
Since 1 ft = 12 inches; thus
12.375 ft/s = (12.375 × 12 ) inches = 148.5 In/s
 5.5 ft/s = 66 In/s
5.5 ft/s = 66 In/s
By using the linear momentum in x-direction for the volume ; we have the relation:
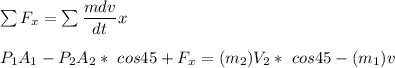
where;
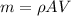
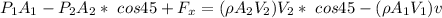
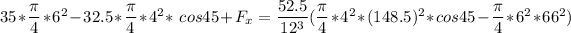
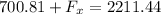
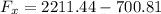
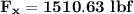
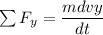

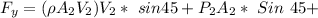
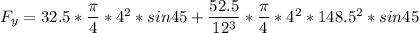
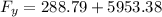
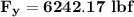
Therefore; the restraining forces in the x and y-directions are :