Question

Determine the estimate of the mean when the process is in control.Assuming the process standard deviation is .50 and the mean of the process is the estimate calculated in Question 1, determine the Upper Control Limit (UCL) and the Lower Control Limit (LCL) for the manufacturing process.Explain the results to the vice-president of the mattress manufacturer focusing on whether, based on the results, the process is in or out of control.

Answer 1

The question is incomplete! Complete question along with answer and step by step explanation is provided below.

Question:

A local mattress manufacturer wants to know if its manufacturing process is in or out of control and has hired you, a statistics expert in the field, to analyze its process. Specifically, the business has run 20 random samples of size 5 over the past month and has determined the mean of each sample.

95.72 95.44 95.4 95.5 95.56 95.72 95.6 95.24 95.46 95.44 95.8 95.2 94.82 95.78 95.18 95.32 95.08 95.22 95.04 95.48

a. Determine the estimate of the mean when the process is in control.

b. Assuming the process standard deviation is .50 and the mean of the process is the estimate calculated in Question 1, determine the Upper Control Limit (UCL) and the Lower Control Limit (LCL) for the manufacturing process.

c. Explain the results to the vice-president of the mattress manufacturer focusing on whether, based on the results, the process is in or out of control.

Answer:

`Mean = \bar{x} = 95.4`

`(LCL, \: UCL) = (94.73, \: 96.07)`

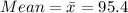
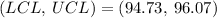
The mean of the 20 random samples of size 5 over the past month lies between the obtained control limit of (94.73, 96.07) therefore, the process is in control.

Step-by-step explanation:

a. Determine the estimate of the mean when the process is in control.

The mean is given by

`Mean = \bar{x} = (\sum x)/(n)`

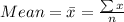
Where n = 20 samples

Using Excel,

=AVERAGE(number1, number2,....)

The mean is found to be

`Mean = \bar{x} = 95.4`

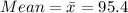
b. Assuming the process standard deviation is .50 and the mean of the process is the estimate calculated in Question 1, determine the Upper Control Limit (UCL) and the Lower Control Limit (LCL) for the manufacturing process.

The Upper Control Limit (UCL) is given by

`$ UCL = \bar{x} + (3 \cdot s)/(√(n) ) $`

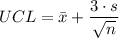
Where
`\bar{x}` is the mean, s is the standard deviation and n is the size of random samples that is 5 (not 20)

`UCL = 95.4 + (3 * 0.50)/(√(5) ) \\\\UCL = 95.4 + 0.671 \\\\UCL = 96.07`

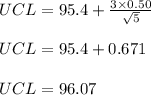
The Lower Control Limit (UCL) is given by

`$ LCL = \bar{x} - (3 \cdot s)/(√(n) ) $`

`LCL = 95.4 - (3 * 0.50)/(√(5) ) \\\\LCL = 95.4 - 0.671 \\\\LCL = 94.73`

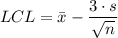
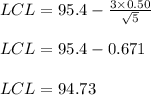
So the control limits are

`(LCL, \: UCL) = (94.73, \: 96.07)`

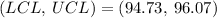
c. Explain the results to the vice-president of the mattress manufacturer focusing on whether, based on the results, the process is in or out of control.

The process is in control based on the obtained results.

The mean of the 20 random samples of size 5 over the past month lies between the obtained control limit of (94.73, 96.07) therefore, the process is in control.