Answer:
651.
Explanation:
Note: In the given series it should be -29 instead of 29 because 29 cannot be a term of AP whose first term is 91 and common difference is -6.
Consider the given series is
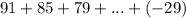
It is the sum of an AP. Here,
First term = 91
Common difference = 85 - 91 = -6
Last term = -29
nth term of an AP is

where, a is first term and d is common difference.
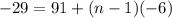
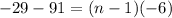
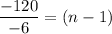

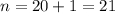
Sum of AP is
![Sum=(n)/(2)[\text{First term + Last term}]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xqvxk7g2pbuewx8cbrintcmmxs0oer4w94.png)
![Sum=(21)/(2)[91+(-29)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/one6tf4jthuq1vl6szi7es4ctc4a5x88cg.png)
![Sum=(21)/(2)[62]](https://img.qammunity.org/2021/formulas/mathematics/high-school/48qsapnotgu530q3v5rmtwddmzmfj2sejw.png)
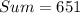
Therefore, the sum of given series is 651.