Question

Find the sum of each series, if it exists
91 + 85 + 79 + … + (­29)

Answer 1

651.

Explanation:

Note: In the given series it should be -29 instead of 29 because 29 cannot be a term of AP whose first term is 91 and common difference is -6.

Consider the given series is

`91+85+79+...+(-29)`

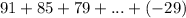
It is the sum of an AP. Here,

First term = 91

Common difference = 85 - 91 = -6

Last term = -29

nth term of an AP is

`a_n=a+(n-1)d`

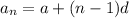
where, a is first term and d is common difference.

`-29=91+(n-1)(-6)`

`-29-91=(n-1)(-6)`

`(-120)/(-6)=(n-1)`

`20=(n-1)`

`n=20+1=21`

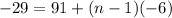
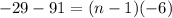
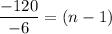
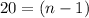
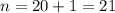
Sum of AP is

`Sum=(n)/(2)[\text{First term + Last term}]`

`Sum=(21)/(2)[91+(-29)]`

`Sum=(21)/(2)[62]`

`Sum=651`

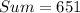
Therefore, the sum of given series is 651.