Question

The time X(mins) for Ayesha to prepare breakfast for her family is believed to have a uniform

distribution with A=25 and B=35.
a) Determine the pdf of X and draw its density curve.
b) What is the probability that time taken by Ayesha to prepare breakfast exceeds 33 mins?
c) What is the probability that cooking or preparation time is within 2 mins of the mean time?
(Hint: Identify mean from the graph of f(x))

Answer 1

(c)
`f_(X)(x)=\left \{ {{(1)/(35-25)=(1)/(10);\ 25<X<35} \atop {0;\ Otherwise}} \right.`

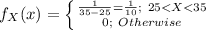
(b) The probability that time taken by Ayesha to prepare breakfast exceeds 33 minutes is 0.20.

(c) The probability that cooking or preparation time is within 2 mins of the mean time is 0.40.

Explanation:

The random variable X follows a Uniform (25, 35).

(a)

The probability density function of an Uniform distribution is:

`f_(X)(x)=\left \{ {{(1)/(B-A);\ A<X<B} \atop {0;\ Otherwise}} \right.`

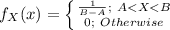
Then the probability density function of the random variable X is:

`f_(X)(x)=\left \{ {{(1)/(35-25)=(1)/(10);\ 25<X<35} \atop {0;\ Otherwise}} \right.`

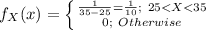
(b)

Compute the value of P (X > 33) as follows:

`P(X>33)=\int\limits^(35)_(33) {(1)/(10)} \, dx \\\\=(1)/(10)\cdot\int\limits^(35)_(33) {1} \, dx \\\\=(1)/(10)* [x]^(35)_(33)\\\\=(35-33)/(10)\\\\=(2)/(10)\\\\=0.20`

Thus, the probability that time taken by Ayesha to prepare breakfast exceeds 33 minutes is 0.20.

(c)

Compute the mean of X as follows:

`\mu=(A+B)/(2)=(25+35)/(2)=30`

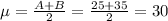
Compute the probability that cooking or preparation time is within 2 mins of the mean time as follows:

`P(30-2<X<30+2)=P(28<X<32)`

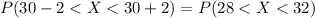
`=\int\limits^(32)_(28) {(1)/(10)} \, dx \\\\=(1)/(10)\cdot\int\limits^(32)_(28){1} \, dx \\\\=(1)/(10)* [x]^(32)_(28)\\\\=(32-28)/(10)\\\\=(4)/(10)\\\\=0.40`

Thus, the probability that cooking or preparation time is within 2 mins of the mean time is 0.40.