Question

Line segment AB¯¯¯¯¯¯¯¯ has endpoints A(−2,6) and B(4,−6). What are the coordinates of the point that partitions BA¯¯¯¯¯¯¯¯ according to the part-to-part ratio 2:4? Enter your answer as an ordered pair, formatted like this: (42, 53)

Answer 1

(2, -2) are the coordinates of the point which divides BA into ration 2:4.

Explanation:

The given two co-ordinates of A are (-2, 6) and B is (4, -6).

Let P be the point that divides the line BA into ratio 2:4.

to find coordinates of a point P on the line segment BA dividing it in a ratio 2:4, we can use segment formula.

`x = (mx_(2)+nx_(1))/(m+n)\\y = (my_(2)+ny_(1))/(m+n)`

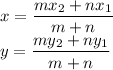
Where (x,y) is the co-ordinate of the point P which

divides the line segment joining the points
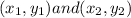`(x_(1), y_(1)) and (x_(2), y_(2))` in the ratio m:n.

Please refer to the attached image.

As per the given values :

`x_(1) = 4\\x_(2) = -2\\y_(1) = -6\\y_(2) = 6\\`

Putting the given values in above formula :

x-co-ordinate of P:

`x = (4 * 4 -2 * 2)/(4+2)\\\Rightarrow (12)/(6)\\\Rightarrow x = 2`

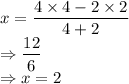
y-co-ordinate of P :

`y = (4 * -6 +2 * 6)/(4+2)\\\Rightarrow (-24+12)/(6)\\\Rightarrow (-12)/(6)\\\Rightarrow y = -2`

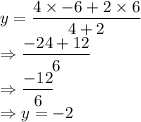
So, answer is P(2, -2).