Question

Your 64-cm-diameter car tire is rotating at 3.4 rev/s when suddenly you press down hard on the accelerator. After traveling 260 m, the tire's rotation has increased to 5.5 rev/s.

What is the tires angular acceleration?

Answer 1

The angular acceleration of the tire is 0.454 rad/s²

Step-by-step explanation:

Given;

initial velocity, u = 3.4 rev/s = 3.4 rev/s x 2π rad/rev

u = 21.3656 rad/sec

final velocity, v = 5.5 rev/s = 5.5 rev/s x 2π rad/rev

v = 34.562 rad/sec

Calculate the value of angular rotation, θ, of the tire

θ = Number of revolutions x 2π rad/rev

θ =
`(260)/(2 \pi r) *(2 \pi \ rad)/(rev)`

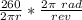
θ = (260 / r)

r is the radius of the tire = 64 / 2 = 32cm = 0.32 m

θ = (260 / 0.32)

θ = 812.5 rad

Apply the following kinematic equation, to determine angular acceleration of the tire;

`v^2 = u^2 + 2 \alpha \theta\\\\2 \alpha \theta = v^2 - u^2\\\\\alpha = (v^2-u^2)/(2 \theta) \\\\\alpha = ((34.562)^2-(21.3656)^2)/(2 (812.5))\\\\\alpha = (738.043)/(1625) \\\\\alpha = 0.454 \ rad/s^2`

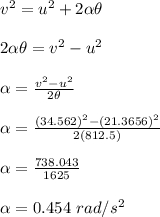
Therefore, the angular acceleration of the tire is 0.454 rad/s²