Question

If 1 P*P = Q6 ( where Q-P=3, then find values of Q and P​

Answer 1

I guess that the equations are:

P*P = Q*6

and

Q - P = 3

now, in the second equation we have:

Q = 3 + P

we can replace it in the first equation:

P^2 = (3 + P)*6 = 6P + 18

then we have the quadratic equation:

P^2 -6P - 18 = 0

Now, we can find the solutions of these equations are:

`P = (+6 +-√((-6)^2 - 4*1*(-18)) )/(2) =(6 +- 10.4)/(2)`

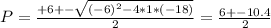
then the solutions are:

P = (6 + 10.4)/2 = 8.2

and

P = (6 - |0.4)/2 = -2.2

Then, if P = 8.2, then we must have Q = 11.2

and if P = -2.2, then Q = 0.8