Answer:
a. P ( X > 12 ) = 0.5254
b. P ( X < 15 ) = 0.7172
c. P ( 9 < X < 13 ) = 0.3179
d. Not unusual
Explanation:
Solution:-
- We will define our random variable X as follows:
X: The weights of the male babies less than 2 month old in USA ( lb )
- The distribution given for the random variable ( X ) is defined to follow normal distribution.
- The normal distribution is identified by two parameters mean ( u ) and standard deviation ( σ ). The distribution is mathematically stated or expressed as:
X ~ Norm ( u , σ^2 )
- The parameters for the normal distribution followed by the random variable ( X ) are given. Hence,
X ~Norm ( 12.3 , 4.7^2 )
- We will use standard normal tables to determine the following probabilities:
a) What proportion of babies weigh more than 12 pounds?
- To use the standard normal tables we need to standardized our limiting value of the required probability by finding the corresponding Z-score value.
- The formula used to compute the Z-score value is given below:
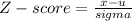
- We are requested to compute the probability p ( X > 12 ). the limiting value is 12 pounds. We will use the conversion formula and compute the Z-score:
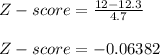
- The standard normal table gives the probabilities of Z-score values in "less than ". So to determine the required probability we look-up:
P ( X > 12 ) = P ( Z > -0.06382 ) = ...
P ( Z > -0.06382 ) = 1 - P ( Z < -0.06382 )
Use standard normal look-up table:
P ( X > 12 ) = 1 - 0.4746
P ( X > 12 ) = 0.5254 ... Answer
Answer: The proportion of babies that weigh more than 12 pounds is the probability of finding babies weighing more than 12 pounds among the total normally distributed population. The proportion is 0.5254
b) What proportion of babies weigh less than 15 pounds?
- We are requested to compute the probability p ( X < 15 ). the limiting value is 12 pounds. We will use the conversion formula and compute the Z-score:
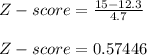
- The standard normal table gives the probabilities of Z-score values in "less than ". So to determine the required probability we look-up:
P ( X < 15 ) = P ( Z < 0.57446 )
P ( X < 15 ) = 0.7172
Answer: The proportion of babies that weigh less than 15 pounds is the probability of finding babies weighing less than 15 pounds among the total normally distributed population. The proportion is 0.7172
c) What proportion of babies weigh between 9 and 13 pounds?
- We are requested to compute the probability p ( 9 < X < 13 ). the limiting value are 9 and 13 pounds. We will use the conversion formula and compute the Z-score:
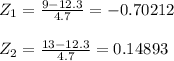
- The standard normal table gives the probabilities of Z-score values in "less than ". So to determine the required probability we look-up:
P ( 9 < X < 13 ) = P ( -0.70212 < X < 0.14893 )
P ( -0.70212 < X < 0.14893 ) = P ( X < 0.14893 ) - P ( X < -0.70212 )
Use standard normal look-up table:
P ( 9 < X < 13 ) = 0.5592 - 0.2413
P ( 9 < X < 13 ) = 0.3179 ... Answer
Answer: The proportion of babies that weigh less than 13 pounds but greater than 9 pounds is the probability of finding babies weighing less than 13 pounds and more than 9 pounds among the total normally distributed population. The proportion is 0.3179
d)
Is it unusual for a baby to weigh more than 18.1 pounds?
- We are requested to compute the probability p ( X > 18.1 ). the limiting value is 18.1 pounds. We will use the conversion formula and compute the Z-score:
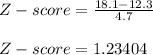
The standard normal table gives the probabilities of Z-score values in "less than ". So to determine the required probability we look-up:
P ( X > 18.1 ) = P ( Z > 1.23404 )
P ( X > 18.1 ) = 0.1086
Answer: The proportion of babies that weight more than 18.1 pounds are 0.1086 of the total babies population. We can say that the proportion of babies that weigh more than 18.1 pounds are significant because the proportion lies is significant. Not enough statistical evidence to be classified as "unusual".