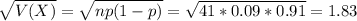Question

In Illinois, 9% of all drivers arrested for DUI (Driving Under the Influence) are repeat offenders; that is, they have been arrested previously for a DUI offence. Suppose 41 people arrested for DUI in Illinois are selected at random. You may assume that this is a binomial distribution.

Required:
a. What is the probability that exactly 3 people are repeat offenders?
b. What is the probability that at least one person is a repeat offender?
c. What is the mean number of repeat offenders?
d. What is the standard deviation of the number of repeat offenders?

Answer 1

a) 21.58% probability that exactly 3 people are repeat offenders

b) 97.91% probability that at least one person is a repeat offender

c) 3.69

d) 1.83

Explanation:

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

The expected value of the binomial distribution is:

`E(X) = np`

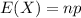
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

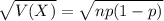
9% of all drivers arrested for DUI (Driving Under the Influence) are repeat offenders

This means that
`p = 0.09`

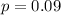
41 people arrested for DUI in Illinois are selected at random.

This means that
`n = 41`

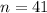
a. What is the probability that exactly 3 people are repeat offenders?

This is P(X = 3).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 3) = C_(41,3).(0.09)^(3).(0.91)^(38) = 0.2158`

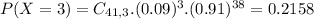
21.58% probability that exactly 3 people are repeat offenders

b. What is the probability that at least one person is a repeat offender?

Either none are repeat offenders, or at least one is. The sum of the probabilities of these outcomes is 1. So

`P(X = 0) + P(X \geq 1) = 1`

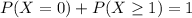
We want
`P(X \geq 1)`.

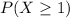Then

`P(X \geq 1) = 1 - P(X = 0)`

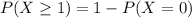
In which

`P(X = 0) = C_(41,0).(0.09)^(0).(0.91)^(41) = 0.0209`

`P(X \geq 1) = 1 - P(X = 0) = 1 - 0.0209 = 0.9791`

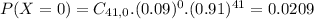
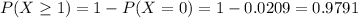
97.91% probability that at least one person is a repeat offender

c. What is the mean number of repeat offenders?

`E(X) = np = 41*0.09 = 3.69`

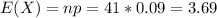
d. What is the standard deviation of the number of repeat offenders?

`√(V(X)) = √(np(1-p)) = √(41*0.09*0.91) = 1.83`