Question

A survey was conducted to find out how many people use public transportation to get to work. The results for 4625 respondents are broken down by gender: 1000 of 2570 males and 1532 of 2055 females use public transportation every working day. Use the information to find the standard error for the difference in proportions of males and females who use public transportation every working day and check the conditions for a normal distribution.

Answer 1

The standard error for the difference in proportions of males and females who use public transportation every working day is 0.015.

The conditions are met.

Explanation:

The sample 1 (males), of size n1=2570 has a proportion of p1=0.389.

`p_1=X_1/n_1=1000/2570=0.389`

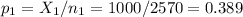
The sample 2 (females), of size n2=2055 has a proportion of p2=0.745.

`p_2=X_2/n_2=1532/2055=0.745`

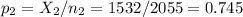
The difference between proportions is (p1-p2)=-0.356.

`p_d=p_1-p_2=0.389-0.745=-0.356`

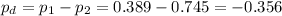
The pooled proportion, needed to calculate the standard error, is:

`p=(X_1+X_2)/(n_1+n_2)=(1000+1532)/(2570+2055)=(2532)/(4625)=0.547`

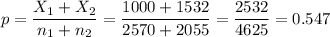
The estimated standard error of the difference between means is computed using the formula:

`s_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.547*0.453)/(2570)+(0.547*0.453)/(2055)}\\\\\\s_(p1-p2)=√(0.000096+0.000121)=√(0.000217)=0.015`

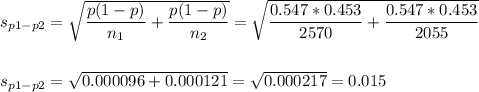
Conditions for a normal distribution approximation:

The expected number of "failures" or "successes", whichever is smaller, has to be larger than 10.

For the males sample, we have p=0.389 and (1-p)=0.611. The sample size is n=2570, so we take the smallest proportion and chek the condition:

`n\cdot p=2570\cdot 0.389=999>10`

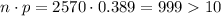
For the females sample, we have p=0.745 and (1-p)=0.255. The sample size is n=2055, so we take the smallest proportion and chek the condition:

`n\cdot (1-p)=2055\cdot 0.255=524>10`

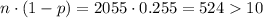
The conditions are met.