Answer:
The standard error for the difference in proportions of males and females who use public transportation every working day is 0.015.
The conditions are met.
Explanation:
The sample 1 (males), of size n1=2570 has a proportion of p1=0.389.
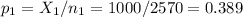
The sample 2 (females), of size n2=2055 has a proportion of p2=0.745.
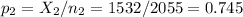
The difference between proportions is (p1-p2)=-0.356.
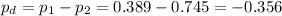
The pooled proportion, needed to calculate the standard error, is:
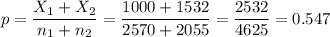
The estimated standard error of the difference between means is computed using the formula:
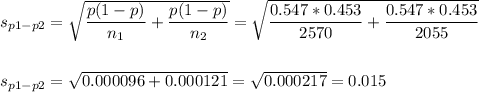
Conditions for a normal distribution approximation:
The expected number of "failures" or "successes", whichever is smaller, has to be larger than 10.
For the males sample, we have p=0.389 and (1-p)=0.611. The sample size is n=2570, so we take the smallest proportion and chek the condition:

For the females sample, we have p=0.745 and (1-p)=0.255. The sample size is n=2055, so we take the smallest proportion and chek the condition:
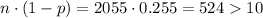
The conditions are met.