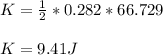Answer:
K = 9.41 J
Step-by-step explanation:
The kinetic energy of a spherical shell is given as:
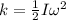
where I = moment of inertia and
ω = angular velocity
Let us find I:
For a hollow sphere:
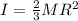
where M = mass = 8.35 kg
R = radius = 0.225 m
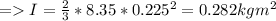
Let us find ω:
Since angular acceleration is constant:
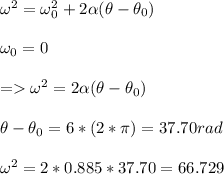
Therefore, its kinetic energy is: